1. Задание № 207 
Сложность: IV
Классификатор алгебры: 3\.9\. Рациональные уравнения, 3\.15\. Уравнения указанных типов, содержащие модуль
Методы алгебры: Метод интервалов , Метод рационализации
Уравнения с модулем
i
Найдите сумму целых решений неравенства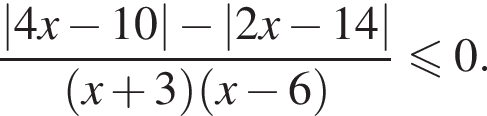 
Решение. Поскольку знак разности 
совпадает со знаком разности 
имеем:
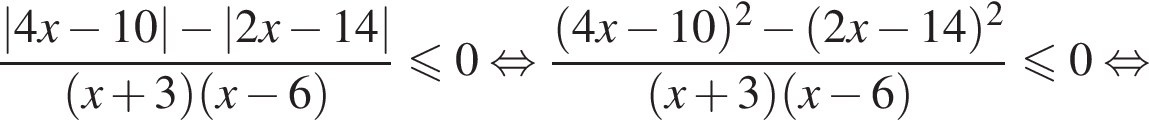
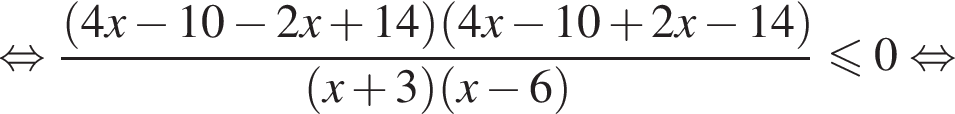
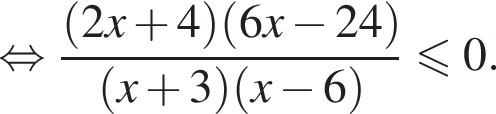
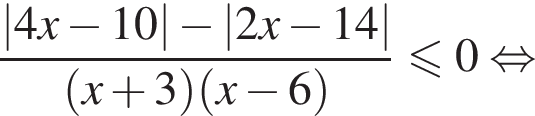
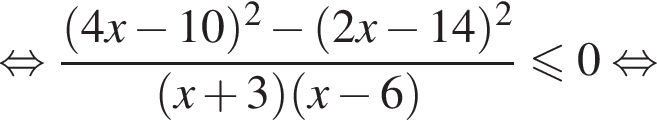
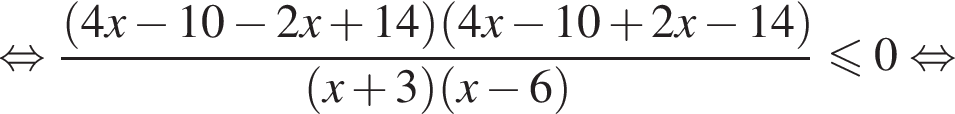
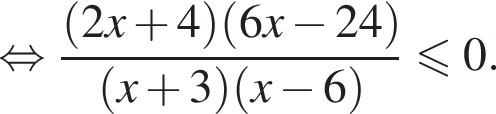
Корни числителя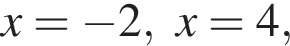 
корни знаменателя 
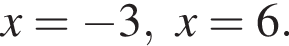Поэтому: 
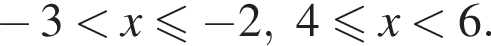Целые решения — числа −2, 4, 5. Их сумма равна 7.
Ответ: 7.
Ответ: 7
207
7
Сложность: IV
Классификатор алгебры: 3\.9\. Рациональные уравнения, 3\.15\. Уравнения указанных типов, содержащие модуль
Методы алгебры: Метод интервалов , Метод рационализации
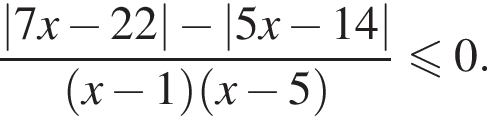
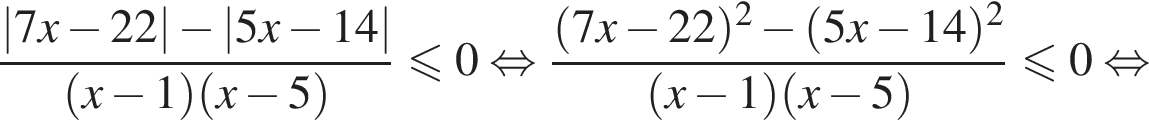
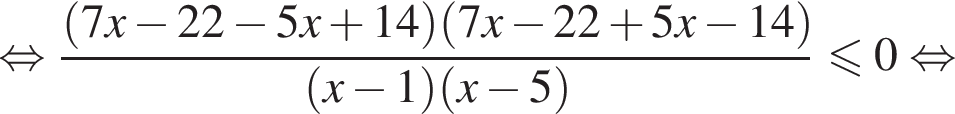
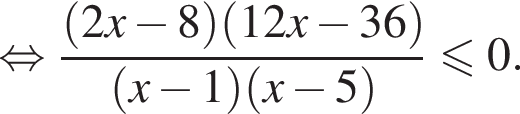
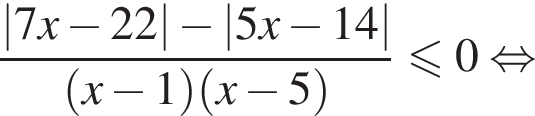
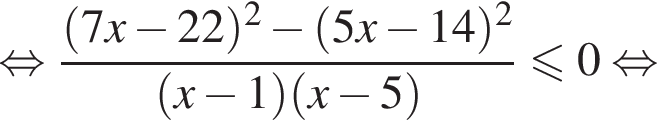
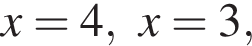корни знаменателя 
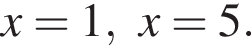Поэтому: 
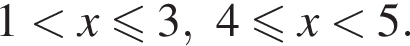Целые решения — числа 2, 3, 4. Их сумма равна 9.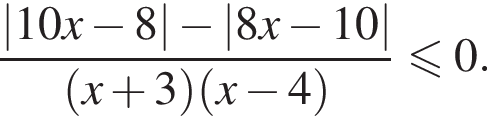
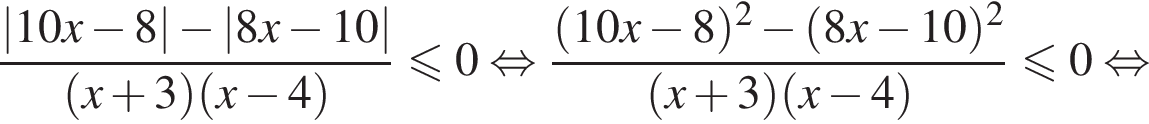
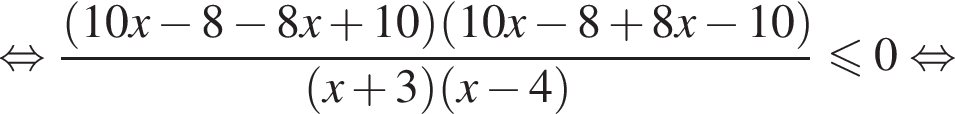
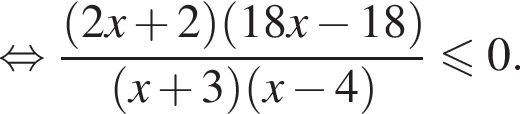
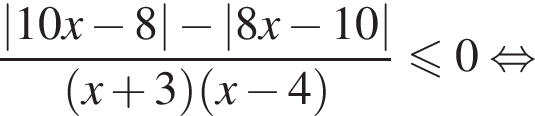
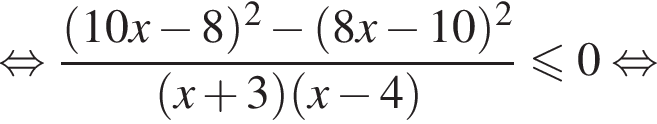
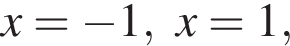корни знаменателя 
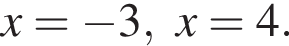Поэтому: 
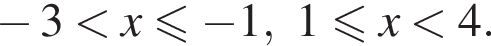Целые решения — числа −2, -1, 1, 2, 3. Их сумма равна 3.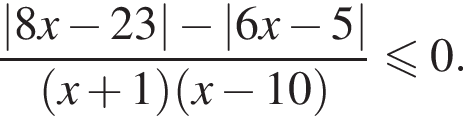
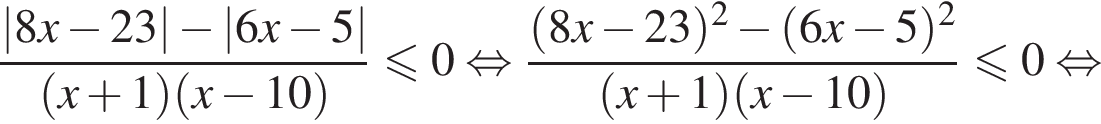
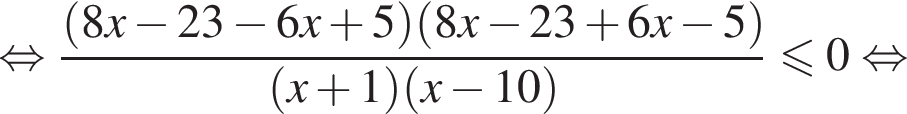
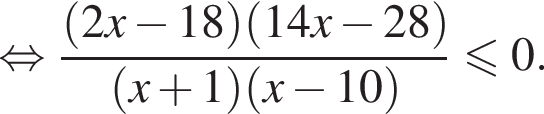
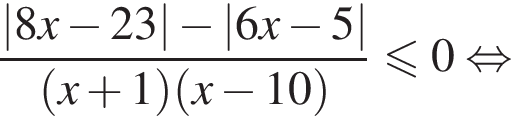
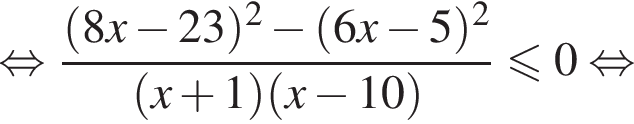
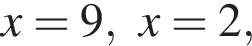корни знаменателя 
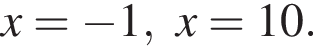Поэтому: 
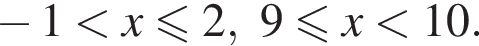Целые решения — числа 0, 1, 2, 9. Их сумма равна 12.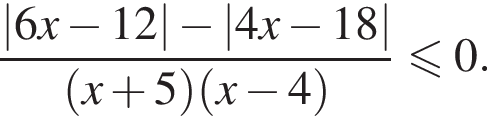
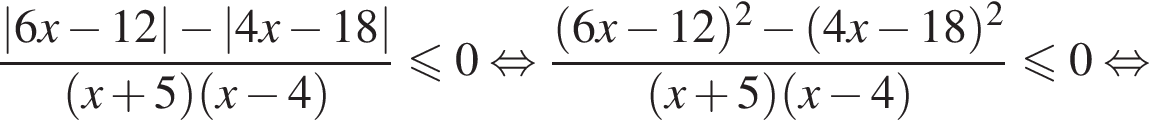
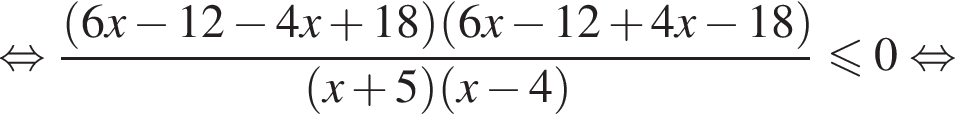
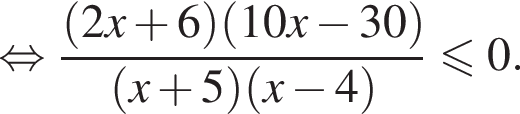
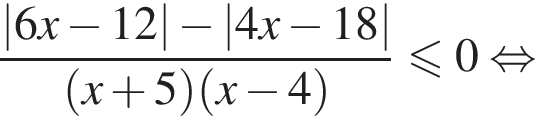
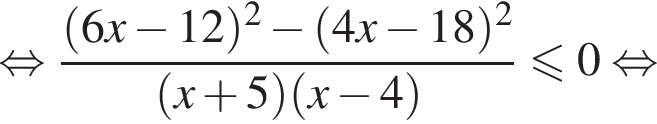
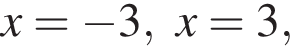корни знаменателя 
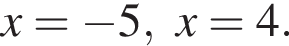Поэтому: 
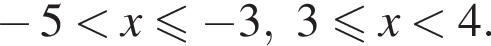Целые решения — числа −4, −3, 3. Их сумма равна −4.